1. Analyse informatique

1.1. Code

L’ensemple du code source est disponible dans le dépôt du projet.

Un paquet de cartes est simplement une liste de nombres (les couleurs sont ignorées).

1@functools.lru_cache()
2def paquet(couleurs=4, valeurs=13):
3    """Crée un paquet de cartes."""
4    return list(itertools.chain.from_iterable(range(valeurs) for _ in range(couleurs)))

Une joueuse peut piocher une carte, et ramasser des cartes.

 1class Joueuse:
 2    """Une joueuse de bataille (et son tas de cartes)."""
 3
 4    def __init__(self, cartes):
 5        self.cartes = list(cartes)
 6
 7    def pioche(self):
 8        """Supprime la première carte du jeu de la joueuse, et la renvoit.
 9
10        :raise Perdu: Lorsque la joueuse n'a plus de cartes à piocher.
11        """
12        try:
13            return self.cartes.pop(0)
14        except IndexError as error:
15            raise Perdu() from error
16
17    def ramasse(self, cartes):
18        """Ajoute les cartes à la fin du tas de la joueuse, dans un ordre aléatoire."""
19        random.shuffle(cartes)
20        self.cartes.extend(cartes)
21
22    def __bool__(self):
23        return bool(self.cartes)

Une partie se joue jusqu’à épuisement des cartes de l’un·e des deux joueur·se·s, et renvoit le nombre de tours joués.

 1def partie(  # pylint: disable=inconsistent-return-statements
 2    _=None, couleurs=4, valeurs=13
 3):
 4    """Joue une partie de bataille, et renvoit sa durée (en nombre de tours)."""
 5
 6    # Les couleurs ne sont pas différenciées (c'est inutile pour la suite).
 7    melange = random.sample(paquet(couleurs, valeurs), k=couleurs * valeurs)
 8    joueuse1 = Joueuse(melange[: len(melange) // 2])
 9    joueuse2 = Joueuse(melange[len(melange) // 2 :])
10
11    for tour in itertools.count(1):
12        try:
13            # Les joueuses piochent une carte
14            table = []
15            carte1 = joueuse1.pioche()
16            carte2 = joueuse2.pioche()
17            while carte1 == carte2:
18                # Bataille
19                # Les joueuses posent leur carte sur la table,
20                # ainsi qu'une autre carte de leur jeu.
21                table.append(carte1)
22                table.append(carte2)
23                table.append(joueuse1.pioche())
24                table.append(joueuse2.pioche())
25                # Les joueuses piochent une nouvelle carte.
26                carte1 = joueuse1.pioche()
27                carte2 = joueuse2.pioche()
28            # Les deux cartes des joueuses sont différentes.
29            # Le gagnant ramasse les cartes
30            # (et celles qui ont été posées sur la table en cas de bataille.).
31            if carte1 > carte2:
32                joueuse1.ramasse([carte1, carte2] + table)
33            else:
34                joueuse2.ramasse([carte1, carte2] + table)
35            if (not joueuse1) or (not joueuse2):
36                raise Perdu()
37        except Perdu:
38            # Un des deux jouers doit piocher une carte, mais son jeu est vide.
39            # La partie est terminée : on renvoit le nombre de tours joués.
40            return tour

1.2. Indicateurs

Voici les indicateurs pour les jeux les plus courants. Toutes les configurations ont été testées, pour un nombre de couleurs inférieur à 10, et un nombre de cartes par couleur inférieur à 10 : voir les données et graphiques, les statistiques.

1.2.1. Jeu de 32 cartes

Sur un million de parties (avec un jeu de 8 cartes de 4 couleur) :

(png, hires.png, pdf)

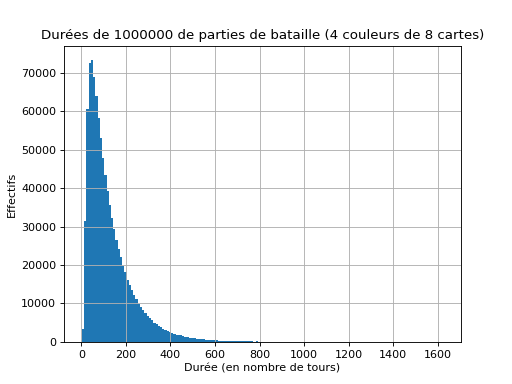
../../_images/informatique-1.png

  • Plus courte partie : 3 plis ; plus longue partie : 1625 plis.

  • Moyenne : 126.5, Médiane : 96.0, Mode : 44.

  • Intervalle de confiance : [20 ; 404].

  • Données brutes.

Interprétation : Une partie dure en moyenne 126,5 plis ; la moitié des parties dure 96 plis ou moins, la moitié dure 96 plis ou plus ; la durée la plus fréquente est 44 plis. Dans 95% des cas, la durée de la partie est comprise entre 20 et 404 plis.

1.2.2. Jeu de 52 cartes

Sur un million de parties (avec un jeu de 13 cartes de 4 couleur) :

(png, hires.png, pdf)

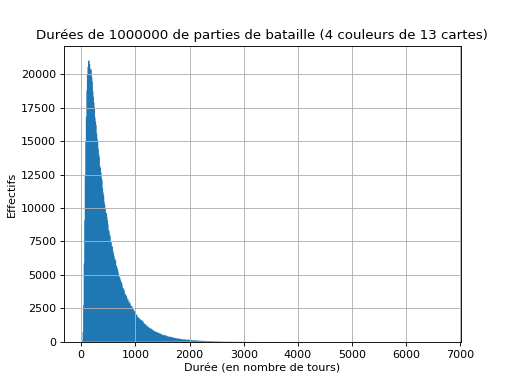
../../_images/informatique-2.png

  • Plus courte partie : 15 plis ; plus longue partie : 6680 plis.

  • Moyenne : 441.4, Médiane : 334.0, Mode : 140.

  • Intervalle de confiance : [70 ; 1414].

  • Données brutes.

1.2.3. Jeu de Bata-waf

Sur un million de parties (avec un jeu de 6 cartes de 6 couleurs) :

(png, hires.png, pdf)

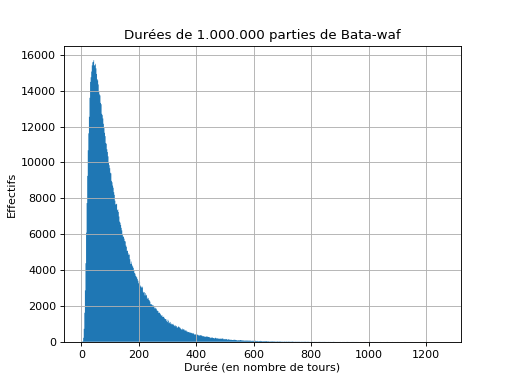
../../_images/informatique-3.png

  • Plus courte partie : 2 ; plus longue partie : 1260.

  • Moyenne : 118.9, Médiane : 90.0, Mode : 40.

  • Intervalle de confiance : [20 ; 374].

  • Données brutes.

1.3. Parité

Une chose qui m’a surpris est que selon mes simulations, la probabilité d’obtenir une durée de partie (en nombre de plis) paire ou impaire n’est absolument pas la même. Dans le graphique suivant, la courbe bleue correspond aux durées de parties paires, alors que la orange aux parties impaires (avec un jeu de 52 cartes).

(png, hires.png, pdf)

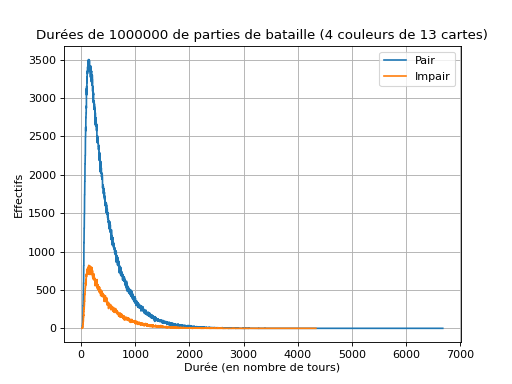
../../_images/informatique-4.png

Je ne comprends ni pourquoi, pour un jeu de 52 cartes, les deux parités ne sont pas équiprobables, ni pourquoi cela dépend du nombre de couleurs et de cartes.

J’ai calculé la parité la plus courante en fonction du nombre de cartes et de couleurs. En ignorant les parties avec peu de cartes ou de couleurs, la règle semble être :

  • Si le nombre de couleurs et le nombre de valeurs sont tous les deux pairs, les parties de durée paire sont les plus probables.

  • Si le nombre de couleurs ou le nombre de valeurs est un multiple de 4, les parties de durée paire sont les plus probables.

  • Si le nombre de couleurs et le nombre de valeurs sont tous les deux impairs, les parties de durée paire et impaire sont à peu près équiprobables.

  • Sinon, si le nombre de couleurs est pair, et le nombre de valeurs est impair, ou l’inverse, les parties de durée paire sont les plus probables.

Je ne sais absolument pas quoi faire de ces affirmations…

1.4. Comparaison

Comme dit plus haut, dans leur article, Delahay et Mathieu n’utilisent pas exactement les mêmes règles que moi. Pour voir la différence, j’ai simulé 1000000 de parties avec mes règles, et avec celles de Delahay et Mathieu. Voici les statistiques obtenues.

Moi

Delahay & Mathieu

Plus courte partie

15

23

Plus longue partie

6680

6955

Moyenne

441,4

582,3

Médiane

334

438

Mode

140

197

Intervalle de confiance

[70 ; 1414]

[92 ; 1872]

Données brutes

Télécharger

Télécharger

Remarquons également que ces statistiques diffèrent grandement de celles annoncées dans leur article : ils obtiennent une durée moyenne de 287 plis (la plus grande partie trouvée ayant 4571 plis), quand je trouve en moyenne 582 plis (la plus grande partie trouvée ayant 6955).

Il est évidemment possible qu’eux ou moi ayons fais des erreurs dans nos simulation. Mais nos résultats diffèrent également à cause de règles du jeu différentes :

  • j’utilise la version dans laquelle, en cas de bataille, chaque joueur·se place une carte face cachée, avant de placer une nouvelle carte face visible pour résoudre la bataille ;

  • dans ma version, les cartes sont ramassées dans un ordre aléatoire, alors que dans leur version, l’ordre est bien précis.

À ma connaissance, ils n’ont pas publié le programme utilisé pour les simulations. Malhreusement, je serais tenté de dire que l’erreur vient de mon côté.

1.5. Usage

Calcule la durée de parties de bataille, et manipule les résultats (affichage au format CSV, calcul de statistiques, tracé de graphiques…).

Par défaut, simule une seule partie et affiche sa durée (en nombre de plis).

usage: bataille [-h] [-V] [-c COULEURS] [-v VALEURS]
                {brut,lscache,plot,stat,multistat} ...

1.5.1. Named Arguments

-V, --version

show program’s version number and exit

-c, --couleurs

Nombre de couleurs du jeu de cartes.

Default: 4

-v, --valeurs

Nombre de cartes dans chaque couleurs.

Default: 13

1.5.2. Sub-commands

1.5.2.1. brut

Calcule les durées de plusieurs parties, et affiche les données brutes au format CSV.

bataille brut [-h]

1.5.2.2. lscache

Affiche la liste des simulations disponibles dans le cache.

bataille lscache [-h]

1.5.2.3. plot

Affiche un graphique des durées des parties.

bataille plot [-h]

1.5.2.4. stat

Calcule les statistiques des durées des parties (une seule configuration).

bataille stat [-h]

1.5.2.5. multistat

Calcule les statistiques des durées des parties (plusieurs configurations).

bataille multistat [-h]

# Simulations sauvegardées

Si ces commandes sont appelées depuis le dépôt git, le résultat de certaines simulation (longues) est recherché dans des fichiers enregistré dans le dépôt plutôt que simulées à nouveau. Cela permet de gagner du temps.

Utilisez bataille cache pour voir la liste des simulations disponibles.

# Nombre de processeurs utilisés

Les simulations sont faites en parallèle. Par défaut, autant de processus que de processeurs sont lancés. Pour modifier cette valeur, définir la variable d’environnement WORKERS au nombre de processeurs utilisés.