1. Analyse mathématique
La première partie (Définitions) propose quelques définitions nécessaires à la lecture de la suite. Les deux parties suivantes sont indépendantes : Combinatoire décrit quelques propriétés des configurations de Dobble, mais ces propriétés ne sont pas utilisées dans la partie Génération de configurations régulières, qui donne l’algorithme utilié pour générer des jeux de tailles arbitrairement grandes. La dernière partie (Bilan), enfin, dresse un bilan de cette analyse.
1.1. Définitions
Commençons par donner quelques définitions.
On se munit d’un ensemble infini d’éléments, appelés symboles.
Une carte est un ensemble de symboles.
Une configuration est un ensemble de cartes.
Une configuration est dite :
valide si :
tout couple de cartes a un et un seul symbole en commun ;
deux symboles quelconques apparaissent exactement une fois sur une même carte.
triviale si elle est constituée de cartes identiques ne contenant qu’un seul symbole, ou d’une unique carte contenant un nombre arbitraire (strictement positif) de symboles (notons qu’une telle configuration est valide, mais peu intéressante pour jouer) ;
régulière si :
chaque symbole apparait autant de fois dans le jeu ;
toutes les cartes possèdent le même nombre de symboles.
Les configurations régulières sont intéressantes car il n’est pas possible d’ajouter une carte, et d’obtenir une configuration valide, sans ajouter un nouveau symbole.
Nous pouvons déjà remarquer qu’il est pertinent de s’intéresser aux configurations valides, triviales et régulières, puisques de telles configurations existent. En voici des exemples (les cadres correspondent aux cartes, et les chiffres sont les symboles).
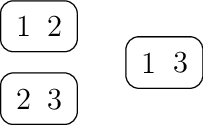
Fig. 1.1 Configuration valide régulière
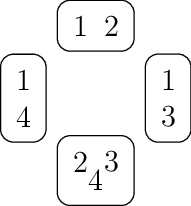
Fig. 1.2 Configuration valide non-régulière
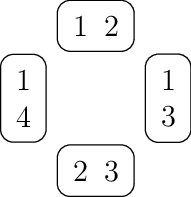
Fig. 1.3 Configuration non-valide
1.2. Combinatoire
1.2.1. Propriétés des configurations régulières
Notons quelques propriétés intéressantes concernant les configurations régulières. Ces propriétés ne seront pas utilisées dans notre algorithme, mais elles éclairent l’ensemble des configurations régulières.
Étant donné une configuration régulière, on nomme :
\(a\) le nombre d’apparition de chaque symbole ;
\(c\) le nombre de cartes ;
\(s\) le nombre de symboles différents ;
\(n\) le nombre de symboles par carte.
Pour toute configuration régulière non triviale, on a :
Les relations \(c\geq2\) et \(n\geq2\) sont de simples reformulations de la définition d’une configuration non triviale.
Puisque \(n\geq2\), alors il y a au moins deux symboles par carte, donc au moins deux symboles différents dans le jeu, donc \(s\geq2\).
Puisque \(c\geq2\), alors il y a au moins deux cartes, donc les symboles apparaissent au moins deux fois (pour mettre en relation les cartes), donc \(a\geq2\).
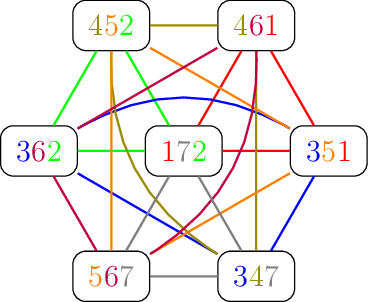
La configuration ci-dessus possède 7 cartes (\(c=7\)) comportant 3 symboles chacune (\(n=3\)), chaque symbole apparaissant 3 fois (\(a=3\)), pour un total de 7 symboles différents (\(s=7\)).
Pour toute configuration régulière, on a la relation \(sa(a-1)=c(c-1)\).
C’est un type de raisonnement classique en combinatoire : compter de deux manières différentes le même ensemble d’objets. Ici, nous comptons le nombre de relations entre les symboles.
On appelle relation entre deux symboles un couple de symboles identiques (qui peut être matérialisé par un segment reliant ces deux symboles), et on compte le nombre de ces relations.
D’une part, chaque symbole est en lien avec \(a-1\) autres symboles, donc pour un type de symbole donné, il y a \(\frac{a(a-1)}{2}\) relations. Multiplié par le nombre de symboles différents \(s\), cela donne \(\frac{sa(a-1)}{2}\).
D’autre part, puisque que pour tout couple de carte, il y a un et un seul symbole en commun, cela signifie qu’il y a exactement une relation entre deux cartes quelconques (et aucune relations à l’intérieur d’une carte). Donc le nombre de relations est égal aux nombre de couples de cartes, soit \(\frac{c(c-1)}{2}\).
Ainsi :
Cette relation donne quelques informations concernant les configurations régulières. Par exemple, le nombre de symboles différents doit être un diviseur du produit \(c(c-1)\) (donc il n’existe pas de configuration régulière à 4 symboles et 6 cartes). Ou encore, une configuration régulière ayant autant de symboles différents que de cartes est forcément triviale.
Pour toute configuration régulière, on a \(nc=as\).
Comptons, de deux manières différentes, le nombre total de symboles de notre jeu.
D’une part, il y a \(c\) cartes comportant chacune \(n\) symboles, donc il y a au total \(nc\) symboles.
D’autre part, il y a \(s\) symboles différents, apparaissant chacun \(a\) fois, ce qui fait un total de \(as\) symboles.
Donc \(nc=as\).
Encore une fois, cela nous donne des informations de divisabilité : par exemple, le nombre de cartes doit diviser le produit \(as\).
Pour toute configuration régulière, on a \(cn(n-1)=s(s-1)\).
Comptons le nombre de couples de symboles sur la même carte.
D’une part, chaque carte possède \(n\) symboles, donc \(\frac{n(n-1)}{2}\) couples de symboles. Multiplié par \(c\) cartes, cela fait \(\frac{cn(n-1)}{2}\).
D’autre part, puisque chaque couple de symbole apparait sur une unique carte, le nombre de couples de symboles sur la même carte est égal au nombre de couples de symboles différents possibles, soit \(\frac{s(s-1)}{2}\).
Donc : \(\frac{s(s-1)}{2}=\frac{cn(n-1)}{2}\), et donc \(s(s-1)=cn(n-1)\).
Pour toute configuration régulière, on a \(n(a-1)=c-1\).
Cette propriété se déduit soit des précédentes, soit en comptant de deux manières différentes le nombre de relations partant d’une unique carte.
Pour toute configuration régulière, on a : \(a(n-1)=s-1\).
C’est une conséquence des égalités \(cn(n-1)=s(s-1)\) (Propriété 1.8) et \(cn=as\) (Propriété 1.7).
Pour toute configuration régulière, on a : \(c+n=s+a\).
C’est une conséquence des égalités \(n(a-1)=c-1\) (Propriété 1.9) et \(a(n-1)=s-1\) (Propriété 1.10).
Pour toute configuration régulière, on a :
Ce bilan donne des propriété intéressante, mais nous pouvons aller encore plus loin.
Pour toute configuration régulière non triviale, on a \(c=s\) et \(n=a\).
Considérons une configuration régulière non triviale.
D’une part, on sait que \(c+n=s+a\), donc \(ca(c+n)=ca(s+a)\) et, en développant, \(c^2a+can=cas+ca^2\).
Mais on a également montré que \(nc=as\), donc, en combinant cela avec l’égalité précédente, cela donne :
\[\begin{split}c^2a+a^2s &= c^2n+ca^2 \\ a^2s-ca^2 &= c^2n - c^2a \\ a^2(s-c) &= c^2(n-a)\end{split}\]Mais nous savons que \(c+n=s+a\), donc \(s-c=n-a\), et, en utilisant cela dans l’égalité précédente :
\[\begin{split}a^2(s-c) &= c^2(s-c) \\ (a^2-c^2)(s-c) &= 0 \\ (a-c)(a+c)(s-c) &= 0\end{split}\]Donc l’une au moins des égalités \(a-c=0\), \(a+c=0\) ou \(s-c=0\) est vraie.
Supposons que \(a+c=0\). Alors \(a=c=0\), et le jeu ne contient aucune carte. C’est impossible.
Supposons que \(a-c=0\), donc que \(a=c\). Nous savons que \(n(a-1)=c-1\). Donc :
\[\begin{split}n(a-1) &= c-1 \\ n(c-1) &= c-1 \\ (n-1)(c-1) &= 0\end{split}\]Donc soit \(n=1\), soit \(c=1\). En français, cela donne : soit le jeu ne contient qu’un symbole par carte, soit il ne contient qu’une seule carte. Dans les deux cas, le jeu est trivial, ce qui est contraire à nos hypothèses. Ce cas là est donc impossible.
Donc le troisième cas, \(s-c=0\), est vrai.
Donc \(s=c\) (en d’autres termes, le jeu a autant de cartes que de symboles différents).
Enfin, nous avons montré que \(n+c=s+a\). Puisque \(s=c\), alors \(n=a\).
Nous pouvons maintenant reprendre le bilan, et le simplifier, ou en enlever les relations qui sont désormais redondantes.
Pour toute configuration régulière, on a :
Il suffit de reprendre l’ensemble des égalités du premier bilan (Propriété 1.12), en utilisant le fait que \(c=s\) et \(n=a\) (Propriété 1.13).
Enfin, cette dernière propriété nous permet, connaissant l’un des quatre paramètres \(n\), \(c\), \(s\), \(a\), d’en déduire les trois autres.
Soit une configuration régulière non triviale. Alors :
La première égalité découle de la formule \(n(n-1)=c-1\) prouvée précédemment (Propriété 1.14).
Pour la seconde égalité, partons le la première. Puisque \(c=n^2-n+1\), alors \(n^2-n+1-c=0\). En considérant que \(n\) est l’inconnue, c’est un trinôme du second degré, de discriminant \(\Delta=(-1)^2-4\times 1\times(1-c)=1-4(1-c)=4c-3\).
Puisque la configuration est non triviale, alors \(c>1\) et \(\Delta\) est strictement positif : le trinôme a deux racines :
\(n_1=\frac{-(-1)-\sqrt{4c-3}}{2\times 1}=\frac{1-\sqrt{4c-3}}{2}\)
\(n_2=\frac{-(-1)+\sqrt{4c-3}}{2\times 1}=\frac{1+\sqrt{4c-3}}{2}\)
Puisque \(4c-3>1\), alors \(\sqrt{4c-3}>1\) et \(n_1<0\). Or \(n_1\) est le nombre de symboles par cartes, nécessairement positif, donc cette solution est à exclure. L’unique solution est donc \(n=\frac{1+\sqrt{4c-3}}{2}\).
De plus, nous pouvons en déduire la parité de certains paramètres.
Soit une configuration régulière non triviale. Alors \(c\) et \(s\) sont des nombres impairs.
En d’autres termes : Une configuration régulière possède un nombre impair de cartes, et un nombre impair de symboles.
Nous avons montré (Propriété 1.14) que \(n(n-1)=c-1\). Or \(n\geq2\), donc \(n\) et \(n-1\) sont des nombres entiers strictement positifs. Donc l’un des deux est pair et l’autre impair, et leur produit est pair. Donc \(c-1\) est pair, et \(c\) est impair.
De plus, \(s=c\), donc \(s\) est aussi impair.
1.2.2. Généralisation
Ces propriétés sont des cas particuliers pour les configurations régulières des relations suivantes, valables pour n’importe quelle configuration valide.
Pour une configuration quelconque, on note :
\(S\) l’ensemble des symboles ;
\(C\) l’ensemble des cartes ;
\(s=\operatorname{card}(S)\) le nombre de symboles différents ;
\(c=\operatorname{card}(C)\) le nombre de cartes ;
\(a_i=\operatorname{card}\left\{j\in C|i\in j\right\}\) (pour \(i\in S\)) le nombre d’apparition du symbole \(i\) ;
\(n_j=\operatorname{card}(j)\) (pour \(j\in C\)) le nombre de symboles sur la carte \(j\).
Pour toute configuration valide, on a alors les relations suivantes :
\(\sum\limits_{i\in S}a_i(a_i-1) = c(c-1)\) est obtenu en comptant le nombre de couples de symboles identiques.
\(\sum\limits_{j\in C}n_j(n_j-1) = s(s-1)\) est obtenu en comptant le nombre de couples de symboles différents sur la même carte.
\(\forall i\in S, \sum\limits_{i\in j\in C} n_j = s+a_i-1\) est obtenu, pour un symbole \(i\) quelconque, en calculant la somme des tailles des cartes contenant ce même symbole.
\(\forall j\in C, \sum\limits_{i\in j} a_i = c+n_j-1\) est obtenu, pour une carte \(j\) quelconque, en calculant le nombre d’apparition de l’ensemble des symboles de cette carte.
\(\sum\limits_{i\in S}a_i = \sum\limits_{j\in C}n_j\) est obtenu en comptant le nombre total de symboles (incluant les répétitions).
1.2.3. Configurations duales
Étant donnée une configuration \(\Delta\), constituée des cartes \(C\), elles-mêmes constituées d’éléments de l’ensemble de symboles \(S\), on appelle dual de \(\Delta\), noté \(\Delta^*\), la configuration :
construite avec des symboles \(C\) ;
constituée des cartes \(\left\{c\in C|s\in c\right\}\), pour \(s\in S\).
En d’autres termes :
les cartes \(C\) de la configuration \(\Delta\) forment les symboles \(S^*\) de la configuration duale \(\Delta^*\) ;
pour chaque symbole de \(\Delta\), l’ensemble des cartes de \(\Delta\) contenant ce symbole constitue une carte de \(\Delta^*\).
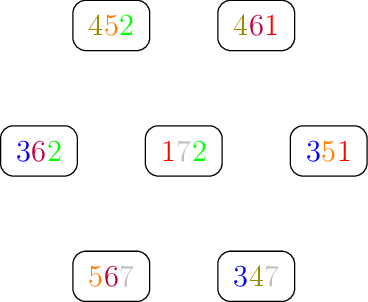
Fig. 1.4 Configuration d’origine
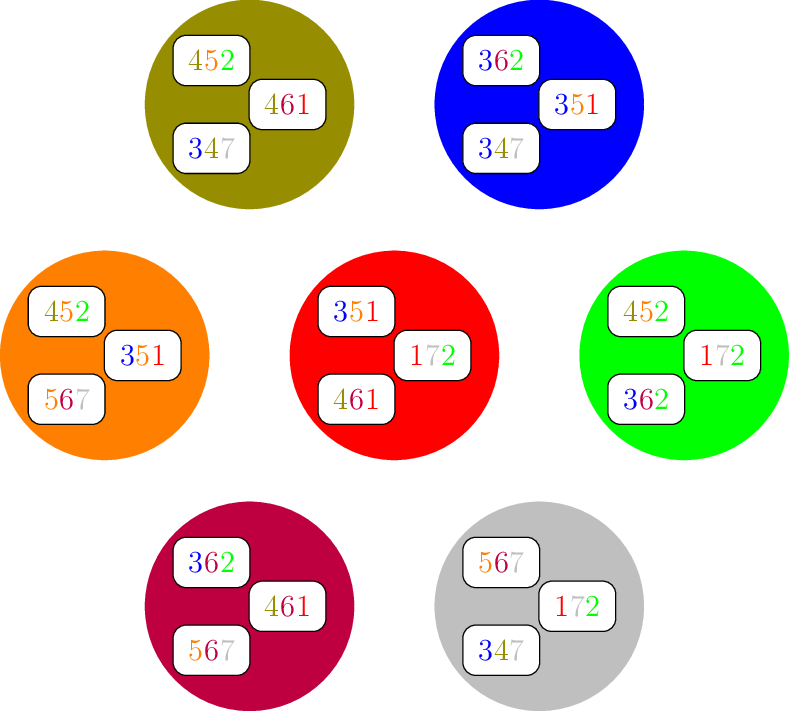
Fig. 1.5 Dual d’une configuration régulière
Pour toute configuration \(\Delta\), en identifiant les cartes de \(\Delta\) aux symboles correspondants, on a : \(\Delta^{**}=\Delta\).
En d’autres termes : le dual du dual d’une configuration est égal à la configuration elle-même.
La démonstration est laissée au lecteur patient.
Le dual d’une configuration \(\Delta\) est valide (respectivement régulière) si et seulement si \(\Delta\) est valide (respectivement régulière).
Soit \(\Delta\) une configuration, constituée de l’ensemble de cartes \(C\) et des symboles \(S\).
Validité
Le fait que deux cartes de \(\Delta^*\) aient exactement un seul symbole commun se traduit par : \(\forall \left(c_1^*, c_2^*\right)\in {C^*}^2 , \operatorname{card}\left(c_1^*\cap c_2^*\right) = 1\).
Or à \(c_1^*\) et \(c_2^*\) correspondent deux symboles \(s_1\) et \(s_2\) de \(\Delta\) (où \(c_1^*\) (resp. \(c_2\)) est l’ensemble des cartes de \(\Delta\) contenant \(s_1\) (resp. \(s_2\))). Donc :
\[\begin{split}c_1^* &= \left\{c\in C|s_1\in c\right\} \\ c_2^* &= \left\{c\in C|s_2\in c\right\} \\\end{split}\]Et donc \(c_1^*\cap c_2^*=\left\{c\in C|s_1\in c \text{ et }s_2\in c\right\}\).
Ainsi, le fait que deux cartes de \(\Delta^*\) aient ayactement un seul symbole commun se traduit par : \(\forall \left(s_1, s_2\right)\in S^2, \operatorname{card}\left\{c\in C|s_1\in c \text{ et } s_2\in c\right\}=1\). En d’autres termes, pour tout couple de symboles de \(\Delta\), il existe une unique carte les contenant tous les deux.
Nous avons montré que la propriété « Tout couple de cartes de \(\Delta^*\) ont exactement un symbole commun » est équivalent à « Tout couple de symboles de \(\Delta\) est présent ensemble dans une unique carte ».
De même, la propriété « Tout couple de cartes de \(\Delta\) ont exactement un symbole commun » est équivalent à « Tout couple de symboles de \(\Delta^*\) est présent ensemble dans une unique carte ». Cela se prouve soit par un argument similaire au précédent, soit en utilisant le fait que \(\Delta^{**}=\Delta\).
Ainsi, \(\Delta\) est valide si et seulement si \(\Delta^*\).
Régularité
Nous supposons maintenant \(\Delta\) valide.
Puisqu’il y a correspondance entre les cartes de \(\Delta\) et les symboles de \(\Delta^*\), et entre les cartes de \(\Delta^*\) et les symboles de \(\Delta\), on a :
chaque symbole de \(\Delta\) apparait autant de fois si et seulement si les cartes de \(\Delta^*\) possèdent le même nombre de symboles ;
les cartes de \(\Delta\) possèdent le même nombre de symboles si et seulement si chaque symbole de \(\Delta^*\) apparait autant de fois.
En d’autres termes, \(\Delta\) étant valide, \(\Delta\) est régulière si et seulement si \(\Delta^*\) est régulière.
Ce lien entre une configuration et son dual n’est pas surprenant si l’on fait, comme Bourrigan, le lien avec la géométrie projective. En effet, Bourrigan voit les configurations valides comme des configurations géométriques, où les symboles sont des droites (ou des cercles), et les cartes des intersections de droites (ou cercles). Or, en géométrie projective, dans une certaine mesure, étant donné une propriété, une propriété analogue existe en considérant des droites et cercles à la place des points, et des points à la place des droites et cercle (voir par exemple l’article de Wikipédia correspondant).
Je m’y connais peu en géométrie projective, mais je pense que la notion de dualité des configurations que nous développons ici est équivalente à la notion de dualité des configurations vue comme des figures de géométrie projective.
Une dernière remarque à propos de cette dualité est que :
le nombre de cartes d’une configuration est égal au nombre de symboles de son dual (et inversement) ;
le nombre d’apparitions d’un symbole d’une configuration est égal au nombre de symboles de la carte correspondante dans le dual (et inversement).
Ainsi, avec cette correspondance, on peut voir dans les relations entre les coefficients démontrées précédemment (Propriété 1.12) plusieurs couples de propriétés duales.
Pour toute configuration régulière, on a :
1.3. Génération de configurations valides
La génération de configurations valides, sans se soucier de leur régularité, est assez aisée, avec par exemple l’algorithme suivant.
L’exemple suivant est la configuration obtenue par l’algorithme avec \(k=9\).
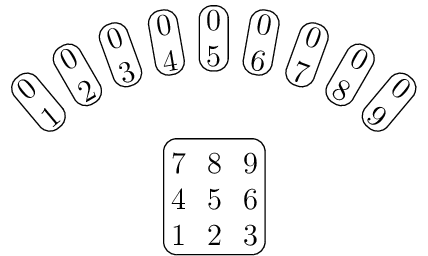
Fig. 1.6 Résultat de l’algorithme avec k=9.
Pour tout entier \(k\geq 2\), on considère comme symboles de la configuration les \(k+1\) entiers de \(0\) à \(k\), et on construit les cartes suivantes :
la carte \(C_0=\left\{1, 2, \ldots, k\right\}\) ;
pour tout entier \(i\in\left[1, k\right]\), la carte \(C_i=\left\{0, i\right\}\).
Pour tout entier \(k\geq 2\), la configuration générée par l’algorithme précédent est valide. De plus, elle est :
régulière si \(k=2\) ;
non régulière si \(k> 2\).
La preuve est laissée au lecteur patient.
Ces configurations sont « faciles » à générer, mais elles ne sont pas intéressantes à jouer : il est assez facile quelle stratégie adopter pour gagner sans avoir à chercher des symboles identiques dans une paire de carte.
Soit \(\Delta_k\) la configuration générée par l’algorithme précédent pour un certain entier \(k\geq 2\), et \(\Delta_k^*\) sa configuration duale. Alors, en identifiant :
le symbole de \(\Delta_k^*\) \(C_0=\left\{1, 2, \ldots, k\right\}\) au symbole \(0\) de \(\Delta_k\) ;
pour tout entier \(i\in\left[1, k\right]\), le symbole de \(\Delta_k^*\) \(C_i=\left\{0, i\right\}\) au symbole \(i\) de \(\Delta_k\) ;
alors :
La preuve est laissée au lecteur patient.
1.4. Génération de configurations régulières
Voici l’algorithme pour générer une configuration régulière, en fonction d’un nombre premier \(p\) (le fait que ce nombre doit être premier sera prouvé par la suite).
1.4.1. Exemple
L’exemple suivant est détaillé sous le graphique.
|
|
1.4.2. Prérequis
Le seul prérequis, outre de l’arithmétique de base, et une certaine aisance avec la lecture de symboles mathématiques, est une connaissance des anneaux \(\mathbb{Z}/n\mathbb{Z}\).
Pour un certain entier \(n\), lorsqu’on fait des calculs dans l’anneau \(\mathbb{Z}/n\mathbb{Z}\), les calculs sont faits modulo \(n\).
Par exemple, dans \(\mathbb{Z}/6\mathbb{Z}\) :
\(10=6+4=4\)
\(7\times 3=21=6\times 3+3=3\)
etc.
1.4.3. Description formelle
Une famille de symboles est un ensemble de symboles, d’intersection nulle avec chacune des autres familles de symboles.
Un tas de cartes est un ensemble de cartes, d’intersection nulle avec chacun des autres tas de cartes.
Un marqueur de tas est un symbole, présent sur toutes les cartes d’un tas, et uniquement sur celles-ci. En d’autres termes, il caractérise le tas.
Dans toute la suite, nous ne manipulons que des nombres entiers, donc les intervalles \(\left[a, b\right]\) désignent les nombres entiers entre \(a\) et \(b\).
Commençons par définir les objets que nous allons manipuler.
\(p\) est un entier naturel non nul.
On se donne les symboles \(d\) (le dernier symbole), \(t_x\), pour \(x\in \left[0, p-1\right]\) (les marqueurs de tas), et \(s_{z,i}\), pour \(z\) et \(i\) dans \(\left[0,p-1\right]\).
L’ensemble \(\left\{t_x|{x\in\left[0,p-1\right]}\right\}\), et, pour tout \(z\in\left[0,p-1\right]\), l’ensemble \(\left\{s_{z,i}|i\in\left[0,p-1\right]\right\}\), sont des familles de symboles.
Chaque \(T_{x,y}\) (pour \(x\) et \(y\) dans \(\left[0,p-1\right]\)) désigne une carte (c’est-à-dire un ensemble de symboles), ainsi que chaque \(S_x\) (pour \(x\in\left[0, p-1\right]\)), et \(T\).
Chaque \(T_x\) (pour \(x\) dans \(\left[0,p-1\right]\)) est un tas contenant l’ensemble de cartes \(\left\{T_{x,y}|y\in\left[0,p-1\right]\right\}\).
Pour \(x\), \(y\), \(z\) dans \(\left[0,p-1\right]\), \(T_{x,y}[z]\) désigne le symbole de rang \(z\) de la carte \(T_{x,y}\).
L’algorithme est illustré dans la figure suivante, et détaillé en dessous.

Commençons par placer les marqueurs de tas. Pour tous \(x\) et \(y\) dans \(\left[0,p-1\right]\), on a \(T{x,y}[p-1]=t_x\). Autrement dit : chaque carte d’un tas \(T_x\) se voit attribuer le marqueur de tas \(t_x\) (et lui seul).
Complétons ensuite les cartes des tas \(T_x\). Pour tous \(x\), \(y\), et \(z\) dans \(\left[0, p-1\right]\), on a \(T_{x,y}[z]=s_{z,xz+y}\) (où l’opération \(xz+y\) est faite dans l’anneau \(\mathbb{Z}/p\mathbb{Z}\)).
La carte \(T\) reçoit les marqueurs de tas \(t_x\) (pour \(x\) dans \(\left[0,p-1\right]\)), ainsi que le dernier symbole \(d\).
Pour tout \(z\) dans \(\left[0,p-1\right]\), la carte \(S_z\) reçoit les symboles \(s_{z,x}\), pour \(x\) dans \(\left[0,p-1\right]\), ainsi que le dernier symbole \(d\).
1.4.4. Preuve
Pour un entier \(p\), la configuration générée par l’algorithme décrit ci-dessus est valide et régulière si et seulement si \(p\) est premier.
Quatre propriétés sont à prouver sur cette configuration, pour en faire une configuration régulière.
Couples de cartes
Par construction, tout couple de cartes parmi les cartes \(\left\{S_z|z\in\left[0,p-1\right]\right\}\) et \(T\) ont un et un seul symbole commun entre elles.
De même, chaque couple d’une carte parmi \(S\cup\left\{T\right\}\) et une carte parmi les \(\left(T_{x,y}\right)_{(x,y)\in\left[0,p-1\right]^2}\) a un et un seul symbole en commun (puisque chaque ligne \(z\) de la figure ne contient que les \(p-1\) symboles \(\left(s_{z,i}\right)_{i\in\left[0,p-1\right]}\), eux mêmes contenus dans la carte \(S_z\), ou, pour la ligne supérieure, que les marqueurs de tas \(\left(t_i\right)_{i\in\left[0,p-1\right]}\), tous contenus dans la carte \(T\)).
Soient deux cartes d’un même tas \(T_x\) (où \(x\in\left[0,p-1\right]\)). Par construction, ces cartes n’ont que le marqueur de tas \(t_x\) en commun.
Restent les couples de cartes de \(\left(T_{x,y}\right)_{(x,y)\in\left[0,p-1\right]}\) appartenant à deux tas différents. Soient deux de ces cartes, \(T_{x_1,y_1}\) et \(T_{x_2,y_2}\), où \(x_1\), \(x_2\), \(y_1\), \(y_2\) sont des nombres de \(\left[0, p-1\right]\), et \(x_1\) et \(x_2\) sont différents. Ces deux cartes contiennent les marqueurs de tas, différents, et respectivement les symboles \(s_{z_1,x_1z_1+y_1}\) et \(s_{z_2,x_2z_2+y_2}\), pour \(z_1\) et \(z_2\) dans \(\left[0,p-1\right]\). Si \(z_2\neq z_2\), alors les deux symboles \(s_{z_1,x_1z_1+y_1}\) et \(s_{z_2,x_2z_2+y_2}\) sont nécessairement différents. Étudions maintenant les symboles \(s_{z,x_1z+y_1}\) et \(s_{z,x_2z+y_2}\), pour un certain \(z\) dans \(\left[0,p-1\right]\). Ils sont égaux si et seulement si \(x_1z+y_1=x_2z+y_2\), c’est-à-dire :
\[\left(x_1-x_2\right)z = y_2-y_1\]De deux choses l’une :
soit \(p\) est un nombre premier, et alors il existe une unique solution \(z=\frac{y_2-y_1}{x_1-x_2}\) (ces calculs se faisant toujours dans \(\mathbb{Z}/p\mathbb{Z}\), qui est alors un corps). Cela signifie que nos deux cartes ont un unique symbole en commun ;
soit \(p\) n’est pas un nombre premier, et alors, pour l’un au moins des quadruplets \(x_1\), \(x_2\), \(y_1\), \(y_2\), l’équation \(\left(x_1-x_2\right)z=y_2-y_1\) a plusieurs solutions (cela est du au fait que \(\mathbb{Z}/p\mathbb{Z}\) n’est alors pas un corps). En conséquence, pour l’un au moins des couples de cartes, il y a plusieurs symboles en commun.
Couples de symboles
Supposons qu’un couple de symboles apparaisse dans deux cartes différentes. Alors ces deux cartes ont plus d’un symbole en commun, et la configuration n’est pas valide, ce qui est contraire à ce qui a déjà été prouvé. Donc chaque couple apparait au plus une fois.
Par construction, chaque symbole \(t_x\), et d, apparaissent une fois avec chacun des autres symboles. Soient deux symboles \(s_{z_1,i}\) et \(s_{z_2,j}\) (\(z_1\neq z_2\)). On pose \(x=\frac{i-j}{z_1-z_2}\) (ce nombre est bien défini si \(p\) est un nombre premier, et \(z_1\neq z_2\)), et \(y=i-xz_1\). Alors \(x\left(z_1-z_2\right)=i-j\), donc \(xz_1-xz_2=i-j\), et enfin \(j-xz_2=i-xz_1\). En notant que \(y=i-xz_1\), nous avons montré \(\left\{\begin{array}{c}y=i-xz_1\\y=j-xz_2\end{array}\right.\). En isolant \(i\) et \(j\) dans ce système, nous obtenons \(\left\{\begin{array}{c}i=xz_1+y\\j=xz_2+y\end{array}\right.\). Donc \(\left\{\begin{array}{c}s_{z_1,i}=s_{z_1,xz_1+y}=T_{x,y}[z_1]\\s_{z_2,j}=s_{z2,xz_2+y}=T_{x,y}[z_2]\end{array}\right.\). Et donc les deux symboles \(s_{z_1,i}\) et \(s_{z_2,j}\) apparaissent tous les deux sur la carte \(T_{x,y}\), aux rangs respectifs \(z_1\) et \(z_2\).
À ce stade, nous avons montré ici que l’algorithme produit une configuration valide si et seulement si \(p\) est un nombre premier.
Nombre d’apparition de chaque symbole
Par construction, chaque symbole apparait \(p+1\) fois, donc chaque symbole apparait autant de fois.
Taille des cartes
Par construction, chaque carte contient \(p+1\) symboles, donc les cartes contiennent autant de symboles.
1.4.5. Mise en œuvre
1def genere_jeu(taille):
2 """Crée et retourne un jeu.
3
4 :param int taille: Taille du jeu.
5 :return: Un jeu.
6 :rtype: :class:`Jeu`
7 """
8 # Est-ce que je sais générer un jeu de cette taille ?
9 if taille != 1 and not est_premier(taille):
10 raise TailleNonGeree(taille)
11
12 # Création des `taille×taille` cartes, réparties en `taille` tas de
13 # `taille` cartes.
14 cartes = [[CarteDobble() for x in range(taille)] for y in range(taille)]
15
16 dernier = 0
17
18 # Affectation des marqueurs de tas
19 marqueurs = list(range(1, taille + 1))
20 for tas in range(taille):
21 for carte in cartes[tas]:
22 carte.symboles.append(marqueurs[tas])
23
24 # Affectation des autres symboles des tas (sauf le dernier)
25 symboles = [
26 list(range(i * taille + 1, (i + 1) * taille + 1)) for i in range(1, taille + 1)
27 ]
28 for x in range(taille):
29 for y in range(taille):
30 for z in range(taille):
31 cartes[x][y].symboles.append(symboles[z][(x * z + y) % taille])
32
33 # Créations des cartes de familles de symboles
34 cartes.append(
35 [CarteDobble(famille + [dernier]) for famille in [marqueurs] + symboles]
36 )
37
38 # Création du jeu à partir des cartes
39 return JeuDobble(itertools.chain.from_iterable(cartes))
1.4.6. Conséquences
Voici quelques conséquences de cet algorithme.
Pour toute configuration régulière (contenant au moins deux cartes), il existe une configuration irrégulière valide (au moins) contenant une carte de moins.
Il suffit d’enlever une carte à une configuration régulière pour obtenir une configuration irrégulière valide.
Il existe un nombre infini de configurations valides, régulières et irrégulières.
Notre algorithme permet de créer une configuration régulière à \(p^2+p+1\) cartes, quel que soit \(p\) premier, et ces configurations sont toutes différentes. Il existe une infinité de nombres premiers (merci Euclide), donc il existe une infinité de configurations régulières.
Les configurations régulières étant valides, il existe une infinité de configurations valides.
Par la propriété précédente, pour chaque configuration régulière, on peut créer une configuration irrégulière ayant une carte de moins. Donc il existe une infinité de configurations irrégulières.
Il existe des configurations valides, régulières, et irrégulières ayant un nombre de cartes, de symboles différents, de symboles total, ou d’apparition de chaque symbole, arbitrairement grand.
Nous avons montré que pour chaque nombre premier \(p\), il existe une configuration régulière, pour laquelle le nombre de cartes, de symboles, etc. est une fonction strictement croissante de \(p\). Donc il existe des configurations régulières de caractéristiques arbitrairement grande.
Il est immédiat que le résultat est de même pour les configurations valides, et irrégulières.
1.5. Bilan
Cette analyse (à la fois combinatoire et algorithmique) était interéssante, ou au moins amusante, mais elle n’est pas complète, et plusieurs questions restent en suspens.
Complétude
Toute configuration régulière est-elle générée par cet algorithme (à permutation des symboles près), ou existe-t-il des configurations qu’il ne capture pas ?
Non. Par exemple, ce programme permet de générer des jeux de Dobble à \(n^2+n+1\) cartes, avec \(n=p^k\), pour n’importe quel couple d’un nombre premier \(p\) et d’un entier \(k\). Notre algorithme ne permet de générer des jeux à \(n^2+n+1\) cartes, où \(n\) est un nombre premier. Cet autre programme peut donc générer un plus grand nombre de jeux que mon algorithme.
La raison est que dans notre algorithme (dont la validité est prouvée dans théorème 1.28), tous les calculs sont faits dans le corps \(\mathbb{Z}/p\mathbb{Z}\) (où \(p\) est un nombre premier). Or cet algorithme pourrait fonctionner dans n’importe quel corps fini, de cardinal \(p^n\) (où \(p\) est un nombre premier, et \(n\) un entier naturel). Il serait alors possible de générer des jeux de dobble à \(n^2+n+1\) cartes (avec \(n=p^k\), pour \(k\) entier) en modifiant l’algorithme pour qu’il travaille dans le corps fini \(\mathbb{F}_q\) (où \(q\) est une puissance d’un nombre premier).
Pour plus d’informations, voir cet article.
Cela ne résout pas le problème du jeu à 157 cartes…
Jeu à 157 cartes
Un cas particulier de cette question, posé par Bourrigan, est le suivant. Existe-t-il une configuration régulière à 157 cartes ? C’est une question ouverte (c’est-à-dire que personne ne sait, dans le monde, si c’est possible).
Notre algorithme ne permet pas de générer une telle configuration, mais cela ne veut pas dire pour autant qu’elle n’existe pas.
D’après le premier algorithme, une configuration valide à 157 cartes existe. Mais ça n’est pas suffisant pour avoir un jeu intéressant, et cela ne répond pas à la question posée par Bourrigan, qui demande (même si nous n’utilisons pas exactement les même définitions) un jeu régulier.
Si une configuration régulière existe, alors, puisque \(c=s=157\), et \(n=a=\frac{1+\sqrt{4\times 157-3}}{2}=13\). Nous pouvons donc affirmer que si une telle configuration régulière existe, alors elle a 157 cartes, 157 symboles, chaque carte contient 13 symboles, et chaque symbole apparait 13 fois. Mais pour que notre algorithme ait pu générer une telle configuration, il aurait fallu que \(p=13-1\) soit premier (puisque pour un nombre premier \(p\), notre algorithme génère un jeu à \(p+1\) symboles par cartes). Mais \(p=12\) n’est pas premier, donc notre algorithme ne peut pas générer une telle configuration.
Nous ne pouvons donc pas affirmer qu’une telle configuration n’existe pas, mais seulement que notre algorithme n’est pas capable d’en générer une.
Géométrie projective
En reprenant l’article de Bourrigan, on peut se demander si les configurations que je génère sont les même que celles qu’il étudie.
C’est partiellement possible :
il se peut que les configurations que je génère sont celles qu’il étudie (mais je ne m’y connais pas assez en géométrie projective pour le prouver) ;
mais puisque qu’il existe des configurations que je ne génère pas (voir plus haut), il étudie davantage de configurations que celles que je suis capable de générer.
Caractère ludique d’une configuration
J’ai l’intuition que pour un nombre de cartes donné, la configuration la plus intéressante à jouer (notion floue) est celle qui contient le plus de symboles par carte. Notre algorithme produit-il ce maximum ?
Histoire
Enfin, je me demande comment les concepteurs du jeu ont créés leur configuration. Ont-il fait une analyse similaire à la mienne ou à celle de Bourrigan ? Ont-ils tatonnés ? Ont-ils une autre méthode ?