euler — Exemples d’application de la méthode d’Euler¶
La méthode d’Euler est une méthode permettant de calculer des solutions approchées d’équations différentielles.
Cet outil fournit différents exemples de mise en œuvre de cette méthode.
Usage¶
Le but de cet outil est de montrer la simplicité de la mise en œuvre de cette méthode. Pour cette raison, les programmes sont réduits à leur strict minimum, et ne contiennent pas d’options. Pour les appeler, lancer l’une des commandes suivantes
euler chute
euler proiepredateur
euler ressort
euler satellite
Principe et Algorithme¶
La méthode d’Euler est utilisée pour trouver une solution approchée d’une équation différentielle. Dans toute cette page, elle permet de tracer point par point une solution approchée de la solution.
Problème¶
Considérons l’équation différentielle suivante :
Pour quelqu’un ayant étudié un tout petit peu les équations différentielles, trouver la solution exacte est simple. Mais il est fréquent, en modélisant des problèmes réels, de devoir résoudre des équations différentielles complexes, dont on ne connaît pas de solution exacte.
Supposons que nous ne connaissions pas la solution exacte. Comment tracer la courbe d’une solution approchée ?
Approximation¶
Prenons la courbe représentative d’une fonction, et sa tangente en une absicsse \(a\) donnée, comme sur l’exemple ci-dessous.
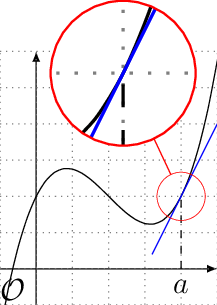
Fig. 13 Une courbe et une tangente
On remarque qu’au voisinnage de l’abscisse \(a\), la corube et sa tangente sont presque confondues. C’est l’approximation faite par la méthode d’Euler.

Fig. 14 Intégration de la fonction x/2 par la méthode d’Euler, Pdebart (source).¶
Premier exemple¶
Reprenons l’équation différentielle précédente.
La solution est la fonction \(x\mapsto e^{0,5\times x}\). Supposons que nous ne connaissons pas cette réponse, et résolvons cette équation sur l’intervalle \([0;1]\) avec la méthode d’Euler, en traçant la courbe sur cet intervalle, avec un pas \(k=0,1\).
Tout d’abord, \(f(0)=1\), donc la courbe passe par le point de coordonnées \((0;1)\).
Ensuite, puisque \(f'(x)=0,5\times f(x)\), alors \(f'(0)=0,5\times f(0)=0,5\), donc l’équation de la tangente à la courbe au point d’abscisse 1 est \(y=0,5 x+1\). Intervient l’approximation de la méthode d’Euler : nous considérons que sur l’intervalle \([0;0,1]\), la courbe de la fonction est confondue avec la tangente, et donc que \(f(0,1)=0,5\times 0,1+1=1,05\). La courbe passe donc par le point de coordonnées \((0,1;1,05)\).
Et nous répétons cette étape. Puisque \(f'(x)=0,5\times f(x)\), alors \(f'(0,1)=0,5\times f(0,1)=0,5\times 1,05=0,525\), donc l’équation de la tangente à la courbe au point d’abscisse \(0,1\) est \(y=0,525x+0,9975\). Nous considérons que sur l’intervalle \([0,1;0,2]\), la courbe de la fonction est confondue avec la tangente, donc \(f(0,2)=0,525\times 0,2+0,9975=1,1025\). La courbe passe donc par le point de coordonnées \((0,2;1,1025)\).
Et ainsi de suite.
Les résultats obtenus sur l’intervalle \([0;1]\) sont visibles dans ce fichier (arrondis à \(10^{-4}\)), ou graphiquement sur le tracé suivant (avec en bleu, la solution exacte).
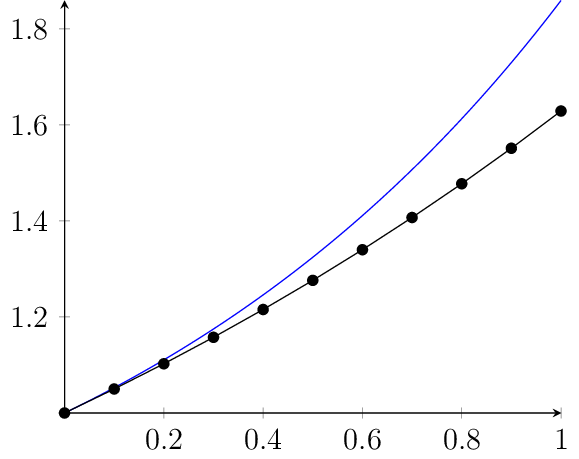
Fig. 15 Solutions exacte et approchée de l’équation différentielle.
Limites¶
Comme on peut le voir sur le graphique précédent, l’erreur d’approximation est de plus en plus élevée. Pour améliorer cela, on peut prendre un pas plus petit, mais ce ne sera jamais parfait.
Si je me souviens bien de mes études, un autre problème de la méthode d’Euler est qu’il ne respecte pas la conservation de l’énergie. Si ce n’est pas forcément très grave pour un jeu vidéo, cela peut poser de gros problèmes au moment d’envoyer une fusée dans l’espace. D’autres méthodes sont alors plus adaptées.
Applications¶
Voici quelques applications mises en œuvre dans ce dépôt.
Chute libre avec rebond¶
La seconde loi de Newton appliquée à un objet en chute libre donne comme équation \(m\overrightarrow{g}=m\overrightarrow{a}\), soit plus simplement \(\overrightarrow{g}=\overrightarrow{a}\), ainsi, sur chacun des deux axes \(x\) et \(y\) (dans un plan vertical contenant la trajectoire), on a :
On considère en plus que lorsque l’objet atteint le sol (\(y<0\)), la vitesse est inversée, et amortie.
La mise en œuvre en Python est donc le code suivant.
1def main():
2 # Position initiale
3 px, py = 0, 0
4 # Vitesse initiale
5 vx, vy = 5, 40
6 # Accélération (qui est constante)
7 ax, ay = 0, -9.81
8
9 h = 0.01
10
11 while True:
12 # Application de la méthose d'Euler
13 px, py, vx, vy = (px + h * vx, py + h * vy, vx + h * ax, vy + h * ay)
14
15 # Rebond
16 if py < 0:
17 py = -py
18 vy = -0.9 * vy
19
20 # Tracé
21 turtle.goto(px, py) # pylint: disable=no-member
Ce qui donne l’exemple de trajectoire suivant.
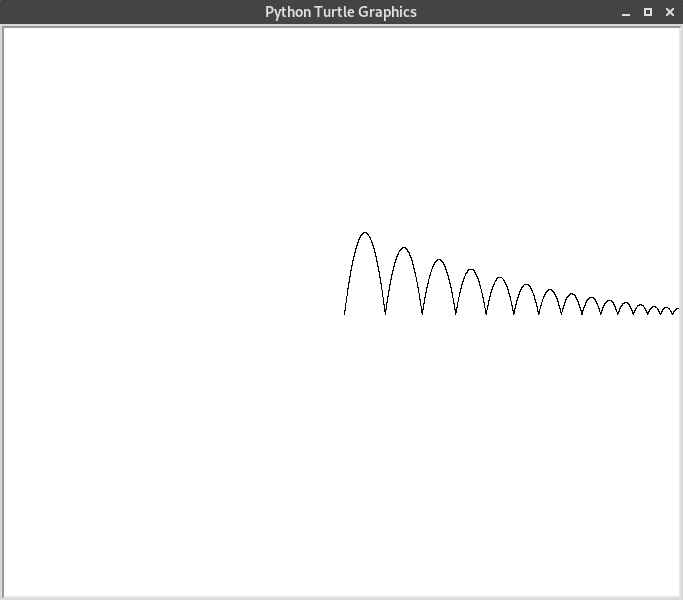
Satellite¶
La seconde loi de Newton appliquée au satellite d’une étoile donne comme équation \(\overrightarrow{P}=m\overrightarrow{a}\), soit (en ne considérant que l’intensité des forces) \(\frac{MG}{d^2}=a\). Ici, \(M\) et \(G\) (masse de l’étoile, et constante universelle de gravitation) sont constante, mais la distance \(d\) entre les deux objets varie en fonction de la position du satellite. L’équation différentielle est donc (avec \(g\) l’intensité de la gravité divisée par le poids, et \(\alpha\) l’angle formé entre l’axe des abscisses, et la droite étoile-satellite) :
La mise en œuvre en Python est donc le code suivant (l’étoile est à l’origine du repère).
1def main():
2 # Position initiale (à droite)
3 px, py = 250, 0
4 # Vitesse initiale (perpendiculaire à l'axe étoile-satellite)
5 vx, vy = 0, 40
6 # Accélération initiale (nulle, mais c'est sans importance)
7 ax, ay = 0, 0
8 # Composante M×m×G de la gravité (unité arbitraire)
9 f = 1000000
10
11 h = 0.001
12
13 turtle.delay(0.1)
14 turtle.up()
15 turtle.goto(px, py)
16 turtle.down()
17
18 while True:
19 # Calcul de la gravité
20 gravite = f / (px**2 + py**2)
21 # Calcul de l'angle entre l'étoile et son satellite
22 angle = atan2(py, px)
23
24 px, py, vx, vy, ax, ay = (
25 px + h * vx,
26 py + h * vy,
27 vx + h * ax,
28 vy + h * ay,
29 -gravite * cos(angle),
30 -gravite * sin(angle),
31 )
32
33 turtle.goto(px, py)
Ce qui donne l’exemple de trajectoire suivant.
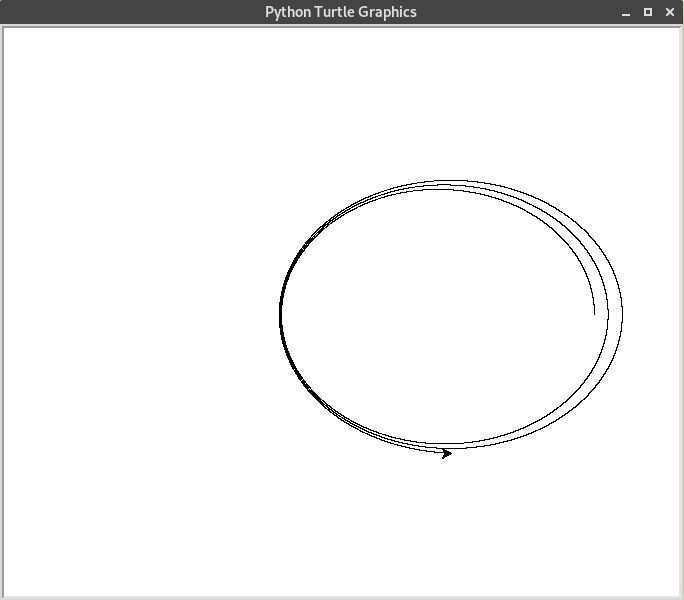
Remarquons que si mes souvenirs sont bons, la solution exacte de cette équation différentielle forme une ellipse parfaite : le satillite devrait revenir exactement à son point de départ. Ce n’est pas le cas ici, à cause des approximations de cette méthode.
Ressort amorti¶
Dans notre système, deux forces sont exercées sur la masse :
la force de traction (ou d’extension) du ressort, d’intensité proportionnelle à son allongement (la différence par rapport à la longueur au repos) ;
les frottements, d’intensité proportionnelle à la vitesse.
L’équation différentielle à résoudre est donc (où \(k\) et \(f\) sont des constantes, ici arbitraires) :
Dans ce cas, j’ai choisi de placer le temps sur l’axe des abscisses, et l’allongement sur les ordonnées. La mise en œuvre en Python est donc le code suivant.
1def main():
2 # Allongement
3 x = 300
4 # Vitesse
5 v = 0
6 # Accélération
7 a = 0
8 # Temps
9 t = 0
10
11 # Coefficient de frottement
12 f = 0.5
13 # Coefficient de la force de rappel
14 k = 20
15
16 h = 0.001
17
18 turtle.tracer(8, 1)
19 turtle.up()
20 turtle.goto(t, x)
21 turtle.down()
22
23 while True:
24 t += 0.02
25
26 x, v, a = (x + h * v, v + h * a, -f * v - k * x)
27
28 turtle.goto(t, x)
Ce qui donne l’exemple de trajectoire suivant.
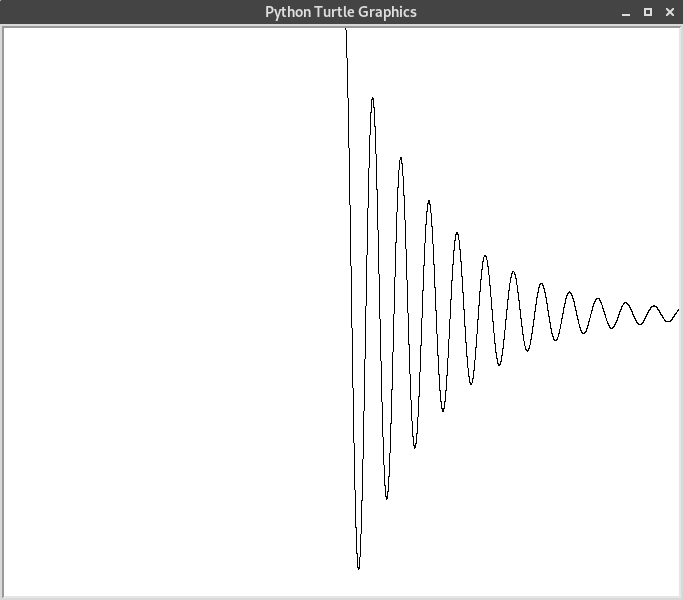
Système proies-prédateurs¶
Lotka et Volterra ont proposé, indépendamment, un modèle de l’évolution des populations de proies et prédateurs. Le système d’équations à résoudre est le suivant (voir la signification des constantes dans l’article de Wikipédia cité précédemment).
La mise en œuvre en Python est donc le code suivant.
1def main():
2 # Définition de trois tortues
3 t_proie = turtle.Turtle()
4 t_predateur = turtle.Turtle()
5 t_phase = turtle.Turtle()
6
7 # Populations
8 n_proie = 50
9 n_predateur = 20
10 # Vitesses de variation des populations
11 v_proie = 0
12 v_predateur = 0
13 # Constantes des équations de Lotka Volterra
14 alpha = 3
15 beta = 0.1
16 gamma = 2
17 delta = 0.1
18
19 t = 0
20 h = 0.001
21
22 # Initialisation des tortues
23 turtle.delay(1) # pylint: disable=no-member
24 t_proie.up()
25 t_proie.goto(t - 200, 5 * n_proie - 200)
26 t_proie.color("green")
27 t_proie.down()
28 t_predateur.up()
29 t_predateur.goto(t - 200, 5 * n_predateur - 200)
30 t_predateur.color("red")
31 t_predateur.down()
32 t_phase.up()
33 t_phase.goto(2 * n_proie - 400, 2 * n_predateur)
34 t_phase.down()
35
36 while True:
37 t += 0.05
38
39 n_proie, n_predateur, v_proie, v_predateur = (
40 n_proie + h * v_proie,
41 n_predateur + h * v_predateur,
42 n_proie * (alpha - beta * n_predateur),
43 n_predateur * (delta * n_proie - gamma),
44 )
45
46 t_proie.goto(t - 200, 5 * n_proie - 200)
47 t_predateur.goto(t - 200, 5 * n_predateur - 200)
48 t_phase.goto(2 * n_proie - 400, 2 * n_predateur)
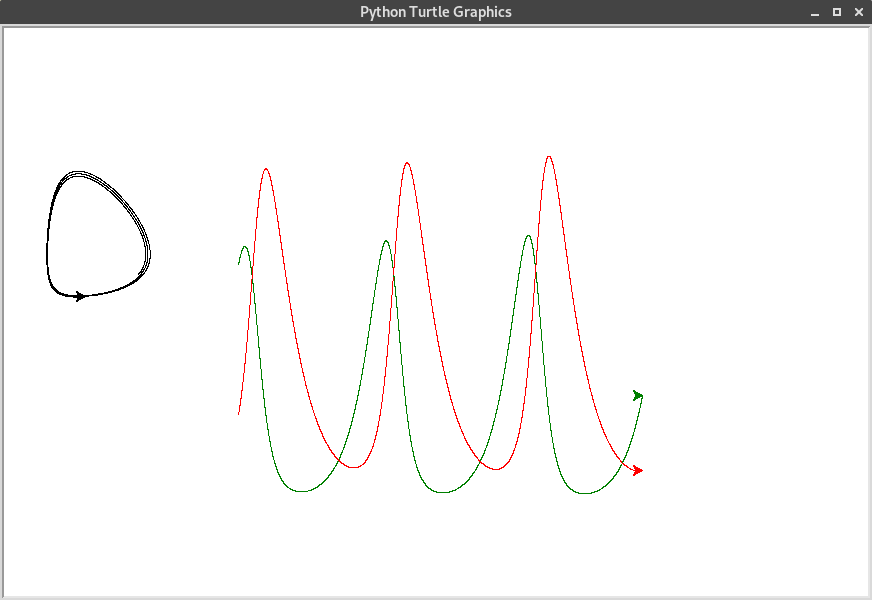
Ce qui donne l’exemple de trajectoire suivant, où :
la courbe verte est celle de la population des proies en fonction du temps ;
la courbe rouge est celle de la population des prédateurs en fonction du temps ;
la courbe noire est la courbe des points \((x(t);y(t))\).
Nous pouvons observer un cycle.
Au départ, les proies sont nombreuses. Les prédateurs ont beaucoup à manger, donc leur population augmente.
Puisque la population des prédateurs augmente, ils mangent de plus en plus de proies, dont la population diminue.
La population de proies n’est plus assez suffisante pour nourrir les prédateurs, dont la population diminue.
Il y a moins de prédateurs, dont la population de proies augmente, ce qui ramène à la population initiale.