panini — Calcul du nombre d’achats nécessaire à compléter un album Panini¶
Suite à une question d’un de ses élèves, une collègue de primaire ma femme m’a demandé combien il faudrait acheter de cartes, en moyenne, pour compléter l’album Panini de One Piece.
Parmi les différents albums disponibles, j’en ai choisi un arbitrairement, et je contineurai cette analyse avec les données suivantes :
pour compléter l’album, il faut 176 stickers (que j’appellerai par la suite cartes, même si c’est incorrect, car les cartes et les stickers sont pour Panini deux choses différentes, mais je suis trop vieux pour comprendre) ;
les cartes stickers se vendent par pochettes de 4.
Je suppose ensuite :
que chaque pochette ne contient que des cartes différentes (il n’est pas possible de trouver deux cartes identiques dans la même pochette) ;
que les cartes sont imprimées en quantité éqale (il n’y a pas de cartes plus rares que d’autres).
État de l’art et Analyse mathématique¶
Je me souvenais avoir entendu parler d’un mathématicien ayant fait ce calcul, et étant arrivé à un prix énorme de l’album complet, et de Panini se défendant en disant « Oui, mais non… C’est plus compliqué que cela… Et en fait il y a aussi les échanges… ».
Je n’ai trouvé que des articles de presse grand public, faisant référence à l’article de l’université de Cardiff [cardiff2018], présentant le travail de Paul Harper, mathématicien de l’institution.
Deux résultats sont présents dans cet article :
en achetant les cartes une à une, le nombre moyen d’achats pour compléter un album de \(n\) cartes est donné par la formule : \(n\left(\ln\left(n\right)+\gamma\right)\), où \(\gamma\) est la constante d’Euler ;
dans l’exemple étudié, les cartes sont achetées par paquet de 5, et il faudra acheter en moyenne 4832 cartes, ou 967 paquets, pour compléter l’album de 682 cartes.
Malheureusement, je n’ai pu trouver aucune preuve ou explications de ce résultat, ni dans l’article lui-même, ni sur la page professionnelle du mathématicien.
J’ai néanmoins pu prouver la première affirmation, et calculer la seconde.
En achetant les cartes une à une, le nombre d’achats nécessaires pour compléter l’album est environ :
Notons \(A_{n,k}\) le nombre moyen d’achats nécessaires pour compléter un album à \(n\) cartes dans lequel il manque encore \(k\) cartes (donc \(n-k\) cartes ont déjà été trouvées). On notera plus simplement \(A_n\) le nombre \(A_{n,0}\), à savoir le nombre moyen d’achats nécessaires pour compléter un album à \(n\) cartes vide.
Pour \(k=0\) : \(A_{n,0}=0\). En effet, l’album n’a aucune carte manquante : aucun achat n’est nécessaire.
Pour toute autre valeur de \(k\), on pioche une nouvelle carte. Deux cas sont alors possibles :
on trouve une nouvelle carte (avec une probabilité \(\frac{k}{n}\)), donc le nombre d’achats est \(1+A_{n,k-1}\) ;
on ne trouve pas de nouvelle carte (avec une probabilité \(\frac{n-k}{n}\)), donc le nombre d’achats est \(1+A_{n,k}\).
Ainsi, on a :
\[\begin{split}A_{n, k} = \frac{k}{n}\times\left(1+A_{n,k-1}\right)+\frac{n-k}{n}\times\left(1+A_{n, k}\right) \\\end{split}\]Isolons \(A_{n,k}\) dans l’égalité précédente.
\[\begin{split}A_{n, k} &= \frac{k}{n}\times\left(1+A_{n,k-1}\right)+\frac{n-k}{n}\times\left(1+A_{n, k}\right) \\ A_{n, k} - \frac{n-k}{n}\times\left(1+A_{n, k}\right) &= \frac{k}{n}\times\left(1+A_{n,k-1}\right)+\frac{n-k}{n} \\ \left(1-\frac{n-k}{n}\right) A_{n, k} &= \frac{k}{n}\times\left(1+A_{n,k-1}\right)+\frac{n-k}{n} \\ \frac{k}{n} A_{n, k} &= \frac{k}{n}\times\left(1+A_{n,k-1}\right)+\frac{n-k}{n} \\ A_{n, k} &= 1+A_{n, k-1}+\frac{n-k}{k} \\ A_{n, k} &= A_{n, k-1}+\frac{n}{k} \\\end{split}\]
Par une démonstration par récurrence dont nous laissons les détails aux lecteur·ice·s patient·e·s, nous avons donc :
l’initialisation : \(A_{n, 0}=0\) ;
l’hérédité : \(A_{n, k}=A_{n, k-1}+\frac{n}{k}\).
Cela nous donne donc :
Or la constante \(\gamma\) étant définie comme :
on se permet l’approximation : \(\sum_{k=1}^n\frac{1}{k}\approx\gamma+\ln(n)\), et en utilisant cette relation dans l’expression de \(A\), on obtient :
Nous avons retrouvé la formule donnée par Paul Harper. Mais pour obtenir son résultat (il faut acheter en moyenne 4832 cartes pour compléter un album de 682 cartes en achetant des paquets de 5 cartes), cette démonstration ne fonctionne plus, car elle supposait d’acheter les cartes une par une.
Une démonstration similaires nous amènerait à une récurrence plus compliquée que celle trouvée ici, qui dépasse mes compétences mathématiques (mais pas celles de Sylvain Sardy et Yvan Velenik [CNRS2020]). Ce calcul est néanmoins à la portée de mes compétences informatiques…
Calcul numérique¶
Préliminaires : Encore un peu de mathématiques¶
Dans cette partie, on note :
\(n\) le nombre de cartes par album ;
\(p\) le nombre de cartes par paquet ;
\(k\) le nombre de cartes manquantes.
À l’ouverture d’un paquet, on peut trouver de \(0\) à \(\min(k, p)\) nouvelles cartes par paquet. Donc, en notant \(P_{n, p, k}(t)\) la probabilité de trouver \(t\) nouvelles cartes dans un paquet donné, le nombre moyen d’achats restant à effectuer est :
Isolons encore une fois \(A_{n, p, k}\) (qui apparait deux fois) dans cette expression.
Il nous reste à calculer \(P_{n, p, k}(t)\) pour pouvoir calculer \(A_{n, p, k}\) par récurrence.
On ouvre un paquet de \(p\) cartes pour compléter un album de \(n\) cartes dans lequel \(k\) sont manquantes, et on souhaite calculer la probabilité d’en trouver \(t\) nouvelles.
La situation est équiprobable. Il y a \(\binom{n}{p}\) conbinaisons possibles de cartes dans le paquet, et parmi celles-ci, le nombre de combinaisons permettant de trouver \(t\) cartes exactement est le produit de :
\(\binom{k}{t}\) : le nombre de combinaisons possibles pour trouver \(t\) nouvelles cartes parmi les \(k\) manquantes ;
\(\binom{n-k}{p-t}\) : le nombre de combinaisons possibles pour que les \(p-t\) cartes restantes du paquet se trouvent parmi les \(n-k\) cartes du paquet déjà trouvées.
Donc la probabilité de trouver exactement \(t\) nouvelles cartes est bien :
Mise en œuvre¶
L’implémentation de cette fonction en Python est la suivante. Elle tire parti de la fonction math.comb(), proposée par le module math de la bibliothèque standard.
1def proba(album, paquet, manquantes, trouvées):
2 """Probabilité de trouver `trouvées` nouvelles cartes dans un paquet.
3
4 :param int album: Nombre total de cartes dans l'album.
5 :param int paquet: Nombre de cartes par paquet acheté.
6 :param int manquantes: Nombre de cartes manquantes dans l'album.
7 :param int trouvées: Probabilité de trouver ce nombre de cartes manquantes dans le paquet.
8 """
9 if trouvées > paquet:
10 return 0
11
12 return (
13 math.comb(album - manquantes, paquet - trouvées)
14 * math.comb(manquantes, trouvées)
15 / math.comb(album, paquet)
16 )
Nous pouvons maintenant écrire la fonction achats(), permettant de calculer \(A_{n,p,k}\). Notre première version était la version récursive suivante.
import functools
@functools.cache
def achats(album, paquet, *, manquantes=None):
"""Calcul du nombre d'achats de cartes nécessaires pour compléter un album.
:param int album: Nombre total de cartes dans l'album.
:param int paquet: Nombre de cartes par paquet acheté.
:param int manquantes: Nombre de cartes manquantes. Si non défini, vaut `album`.
"""
if manquantes is None:
manquantes = album
return (
sum(
proba(album, paquet, manquantes, k) * (1 + achats(album, paquet, manquantes - k))
for k in range(1, 1 + min(paquet, manquantes))
)
+ proba(album, paquet, manquantes, 0)
)
/ (1 - proba(album, paquet, manquantes, 0))
)
Cette fonction calcule correctement la valeur demandée (en notant que la mémoïsation est utilisée grâce au décorateur functools.cache() de la bibliothèque standard), mais au prix d’un haut niveau de récursion, et pour des valeurs de album relativement faibles, Python lève l’exception RecursionError. C’est la raison pour laquelle la version mise en œuvre n’est pas récursive, mais utilise une liste cache dans laquelle sont calculées les valeurs \(A_{n, p, k}\) pour toutes les valeurs de \(k\) jusqu’à \(n\).
1def achats(album, paquet):
2 """Calcul du nombre d'achats de cartes nécessaires pour compléter un album.
3
4 :param int album: Nombre total de cartes dans l'album.
5 :param int paquet: Nombre de cartes par paquet acheté.
6 """
7
8 # `cache[k] = n` signifie :
9 # il faut acheter en moyenne `n` paquets pour compléter un album
10 # dans lequel `k` cartes manquent.
11 cache = [0]
12
13 for manquantes in range(1, album + 1):
14 cache.append(
15 (
16 sum(
17 proba(album, paquet, manquantes, k) * (1 + cache[manquantes - k])
18 for k in range(1, 1 + min(paquet, manquantes))
19 )
20 + proba(album, paquet, manquantes, 0)
21 )
22 / (1 - proba(album, paquet, manquantes, 0))
23 )
24
25 return paquet * cache.pop()
Une fois ce projet installé, cette fonction peut être installée en utilisant : panini achats ALBUM PAQUET.
Notons au passage que c’est cet algorithme, non récursif, qui est implémenté en javascript dans cette application.
Réponse¶
Nous pouvons enfin calculer la réponse à notre question.
$ python -m jouets.panini achats 176 4
1004.9276452739583
Pour compléter notre album de 176 cartes en achetant des pochettes de 4 cartes, il faudra acheter en moyenne 1005 cartes (soit 251 pochettes). À un euro la pochette, cela fait un album à 251 €…
Analyse¶
Nous pouvons maintenant étudier comment la taille des paquets de carte influe sur le nombre de cartes à acheter pour compléter l’album. Le graphique suivant présente cela, avec un album de 176 cartes.
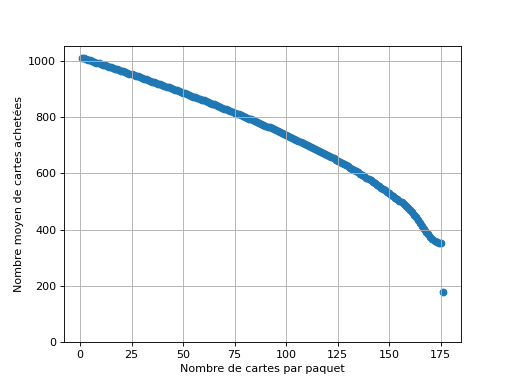
Fig. 19 Nombre moyen de cartes à acheter pour compléter un album de 176 cartes, en fonction du nombre de cartes par paquet¶
Nous voyons qu’augmenter un peu la taille des paquets ne diminue pas sensiblement le nombre de cartes à acheter : par exemple, il faut des paquets de 150 cartes environ (pour un album de 176) pour que le nombre de cartes achetées pour compléter l’album soit divisé par deux (par rapport à des cartes achetées une à une).
Simulations¶
Les 1004 paquets de cartes achetées pour compléter l’album de 176 sont une moyenne. Mais dans quelle mesure peut-on s’éloigner de cette moyenne ? Pour cela, au lieu de calculer la moyenne théorique, nous allons faire des simulations. Le sous-programme panini simulation permet cela. Il utilise la fonction suivante.
1def simule(album, paquet): # pylint: disable=inconsistent-return-statements
2 """Simule l'achat de paquets de cartes jusqu'à obtention du paquet complet.
3
4 :param int album: Nombre total de cartes dans l'album.
5 :param int paquet: Nombre de cartes par paquet acheté.
6 :return: Nombre de *paquets* achetés.
7 """
8 manquantes = album
9 for essais in itertools.count(1):
10 manquantes -= sum(
11 1 for carte in random.sample(range(album), k=paquet) if carte < manquantes
12 )
13 if not manquantes:
14 return essais
Nous utilisons une astuce pour simplifier la fonction : au lieu de nous rappeller quelles cartes ont été trouvées, et quelles cartes sont manquantes, nous définissons la variable manquantes qui correspond au nombre de cartes manquantes. Pour connaître le nombre de nouvelles cartes ont été trouvées à l’ouverture d’un paquet donné, on tire paquet nombres ( le nombre de cartes dans un paquet)entre 0 et album-1, et on considère qu’une nouvelle carte a été trouvée si un des nombres est inférieur à manquantes.
Ainsi, les probabilités sont respectées, mais le calcul nécessite (un peu) moins de mémoire, et devrait fonctionner (un peu) plus rapidement.
Le graphique suivant présente l’effectif du nombre de paquets achetés avant de compléter l’album pour 100000 simulations.
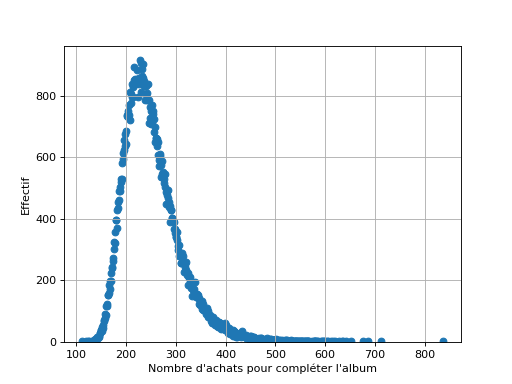
Fig. 21 Après 100000 simulations (d’achats de paquets de 4 cartes pour compléter un album de 176 cartes), effectif du nombre d’achats permettant de compléter l’album.¶
La moyenne théorique est celle calculée à la partie précédente : 251. Comme attendu, la courbe est centrée autour de cette valeur : il est plus probable d’avoir une valeur expérimentale proche de cette moyenne qu’éloignée.
L’intervalle de fluctuation à 95% de la série du graphique précédent est : \(\left[170; 385\right]\). En d’autre termes, il est très peu probable d’avoir le paquet complet de 177 cartes avec moins de 170 paquets achetés (soit 680 cartes), et très peu probable de nécessiter plus de 385 achats de paquets (soit 1540 cartes).
Et les échanges ?¶
L’argument de Panini à ce genre de calculs (qui montre que le prix d’un album complet est très élevé) est : les échanges. En échangeant les cartes en double avec d’autres personnes, il devrait être possible de compléter plus rapidement l’album.
Mettons cette affirmation à l’épreuve.
Encore une fois, l’analyse mathématique a été effectuée par Sylvain Sardy et Yvan Venelik [CNRS2020] ; je propose ici une simulation informatique.
Contrairement à la simulation précédente, aucune astuce ici. La variable manquantes est un compteur des cartes manquantes (par exemple, manquantes[4] == 3 signifie qu’il manque 3 exemplaires de la carte numéro 4). Nous utilisons avantageusement la classe Counter de la bibliothèque standard, qui permet de facilement compter des choses, soustraire un compteur à un autre, et ne conserver que les valeurs positives. La simulation s’arrête lorsque toutes les cartes ont été trouvées, c’est-à-dire lorsque la somme des valeurs de manquantes est nulle.
1def simule(album, paquet, amis): # pylint: disable=inconsistent-return-statements
2 """Simule l'achat de cartes pour compléter plusieurs albums.
3
4 :param int album: Nombre total de cartes dans l'album.
5 :param int paquet: Nombre de cartes par paquet acheté.
6 :param int amis: Nombre d'albums à compléter.
7 :return: Nombre moyen de *paquets* achetés par album, c'est à dire :
8 (nombre de paquets achetés) * (nombre de cartes par paquet) / (nombre d'amis)
9 """
10 manquantes = collections.Counter({carte: amis for carte in range(album)})
11
12 for achats in itertools.count(0):
13 if manquantes.total() == 0:
14 return achats
15
16 # Simule un tirage
17 manquantes -= collections.Counter(random.sample(range(album), k=paquet))
18 # Supprime les valeurs négatives
19 # pylint: disable=pointless-statement
20 +manquantes
Voici le graphique qui présente le nombre de moyen de cartes achetées par personne pour compléter un album de 176 cartes vendues par paquets de 4, en fonction du nombre de personnes. À chaque fois, 1000 simulations ont été réalisées.
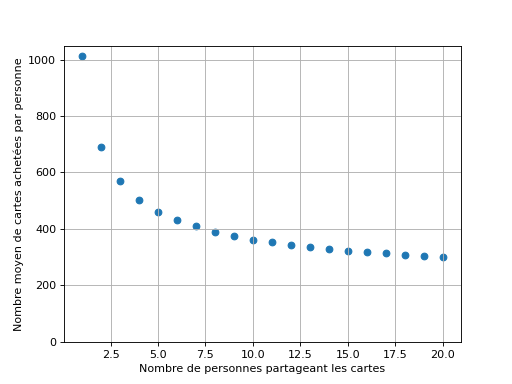
Fig. 23 Nombre moyen de cartes à acheter (par paquet de 4) pour chacune des personnes pour compléter un album de 176 cartes en fonction du nombre de personnes mettant leurs cartes en commun¶
On peut observer sur ce graphique que le nombre de cartes à acheter par personne diminue très rapidement : dés quatre personnes, chacun·e doit acheter deux fois moins de cartes que s’il ou elle était seul. Et avec beaucoup de personnes ?
$ python -m jouets.panini echanges 176 4 1000 1000
191
Ce résultat signifie que, selon ce tirage simulé 1000 fois, 1000 personnes mettant en commun leurs cartes n’auraient besoin d’acheter que 191 cartes chacune pour compléter leur album de 176 cartes, soit 15 doublons par personne.
Conclusion¶
Tout ça est distrayant, mais la seul conclusion est : acheter des cartes au hasard pour compléter son album n’est vraiment pas rentable…
Notes et Références¶
Word Cup Stickers, 28/03/2018, https://www.cardiff.ac.uk/news/view/1136091-world-cup-stickers
Petite collection d’informations utiles pour collectionneur compulsif, Sylvain Sardy et Yvan Venelik, 6 juin 2020, https://images.math.cnrs.fr/Petite-collection-d-informations-utiles-pour-collectionneur-compulsif