Dimension 1,5¶
Alors que je m’ennuyais en formation, j’ai fait ce que je reproche à mes élèves : j’ai gribouillé sur mon cahier au lieu d’écouter.
Je voulais m’amuser avec des automates cellulaires, mais je n’avais qu’un papier et un crayon à disposition : le jeu de la vie est trop compliqué à exécuter à la main (et demande trop de papier). J’ai donc essayé de créer un automate cellulaire à une seule dimension (sur une seule ligne).
Je n’ai pas réussi ; je suis donc passé à deux lignes. Pour déterminer l’état d’une cellule (vivante ou morte) à une étape, on regarde le nombre de cellules l’entourant dans les deux étapes précédentes, comme illustré dans l’exemple suivant.
Premières règles¶
Pour déterminer l’état d’une case à la ligne suivante, on compte le nombre de cellules vivantes l’entourant. Une case :
entourée d’aucune, une ou cinq cellules (le maximum), meurt ou reste vide (d’isolement ou surpopulation) ;
entourée de deux ou trois cellule, reste vivante, ou nait ;
entourée de quatre cellules, conserve le même état.
Cela donne l’exemple suivant, dans lequel les lignes les plus hautes sont les plus vieilles. Pour calculer la troisième ligne, on compte, dans la deuxième ligne, le nombre de cellules vivantes entourant chaque case (ce nombre est indiqué dans l’exemple) ; la nouvelle ligne (en bas) est complétée en conséquence.
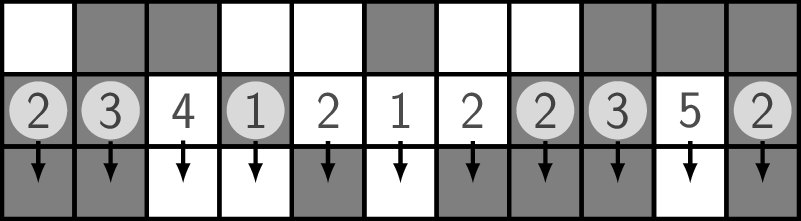
Fig. 5 Calcul d’une ligne.
Ces règles dessinent ce genre de motifs. On y voit une certaine régularité (le même genre de formes reviennent) et un certain aléa.

Fig. 6 Règles originales : –++=-¶
D’autre règles¶
Les règles utilisées précédemment sont « naaturelles » (elles simulent des cellules réelles, qui meurent de surpopulation ou d’isolemnt). En jouant avec d’autre règles, on trouve d’autres motifs intéressants.
Dans toute la suite, les règles sont données sous la forme d’une chaîne du type ++–+= signifiant :
une case entourée de 0 cellules vivantes devient vivante (premier caractère : +) ;
une case entourée de 1 cellules vivantes devient vivante (second caractère : +) ;
une case entourée de 2 cellules vivantes devient morte (troisième caractère : -) ;
etc.
Voici les exemples. Les scénarios font référence à l’option –scenario de la commande.
Les règles suivantes génèrent des planeurs: =-+-=+.

Fig. 7 Règles du scénario « planeur » : =-+-=+¶
Scénario 4 :

Fig. 8 Règles du scénario « 4 » : +-++-+¶
Scénario 5 :

Fig. 9 Règles du scénario « 5 » : +-+-=-¶
Scénario 10 :

Fig. 10 Règles du scénario « 10 » : +-=+-=¶
Scénario 20 :

Fig. 11 Règles du scénario « 20 » : +=+=+-¶
Scénario 40 :

Fig. 12 Règles du scénario « 40 » : –+=-+¶
Voir aussi¶
Je ne suis évidemment pas le seul à avoir imaginé un automate minimaliste. En prenant en compte l’ordre des cellules (et non pas seulement le nombre de cellules vivantes), il est possible de faire un automate cellulaire intéressant à une seule dimension : la règle 110.